El modelo busca encontrar las variables relevantes que ocasionan el crecimiento económico de un país (economía cerrada), en cuanto algunas ayudan a mejorar la situación solo en el corto plazo, y otras, que afectan a las tasas de crecimiento del largo plazo. Se toman todas las variables que el modelo considera como significativas en el proceso de crecimiento, como exógenas, pero muestra la incidencia de estas en el proceso de crecimiento. El modelo utiliza la función de producción Cobb-Douglas: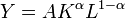
Definiendo las variables, tenemos que:
K = Capital total
L = Fuerza laboral o trabajo total usado en la producción.
A = es una constante matemática que depende del nivel de tecnología.
Y = Producción total [medida por ejemplo en unidades monetarias].
α = Fracción del producto producida por el capital, o coeficiente de los rendimientos marginales decrecientes.
Se sabe, por otro lado, que necesariamente , se puede probar que α coincide con la participación total del capital en la producción (de acuerdo con el análisis de la productividad total de los factores). Si alfa es α ~ 1, la producción se basará fundamentalmente en el capital disponible y será casi independiente de la mano de obra. Existen razones para suponer que para muchas situaciones reales la función de producción de Cobb-Douglas es una función creíble de producción que tiene retornos constantes a escala, y rendimientos marginales decrecientes al capital y al trabajo. Más adelante se verá que si se supone que la función de producción es de este tipo, exite la posibilidad de convergencia a un producto estacionario que deja de crecer mediante la tasa de ahorro.
Técnicamente la hipótesis de que la función de producción es la función de Cobb-Douglas no es fundamental para el modelo, porque bastaría que fuera una función monótona creciente en el capital y la cantidad de trabajo.
Para formular el modelo a partir de la función de Cobb-Douglas se definen por conveniencia:
• El producto per cápita efectivo y como la cantidad de producción por unidad de mano de obra y
• El stock de capital per cápita efectivo k como la cantidad de capital por unidad de mano de obra
Es decir, definimos las variables:
Técnicamente la hipótesis de que la función de producción es la función de Cobb-Douglas no es fundamental para el modelo, porque bastaría que fuera una función monótona creciente en el capital y la cantidad de trabajo.
Para formular el modelo a partir de la función de Cobb-Douglas se definen por conveniencia:
• El producto per cápita efectivo y como la cantidad de producción por unidad de mano de obra y
• El stock de capital per cápita efectivo k como la cantidad de capital por unidad de mano de obra
Es decir, definimos las variables:
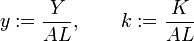
Como hemos supuesto que la función de producción es de tipo Cobb-Douglas se tiene la siguiente relación entre y y k:
Asumiendo el producto per cápita efectivo y en la función anterior, tendremos que mientras menor sea α habrá un producto per cápita efectivo cada vez menor, es decir, la función toma la forma de una raíz, aunque la función es divergente al infinito si k tiende al infinito. La función anterior satsiface las condiciones de Inada, a saber:
Estos límites son conocidos como las condiciones de Inada, y explican que la derivada de , es decir, el producto marginal del capital es 0 cuando k es alto. Además explica que cuando k es demasiado bajo, el producto marginal es muy alto. Estas últimas condiciones, aunque bastante evidentes matemáticamente, posteriormente implicarán que países con una cantidad de capital baja crecerían a tasas altas, mientras que países con altas cantidades de capital crecerían a tasas más bajas, debido a los rendimientos marginales decrecientes de este.
Comentarios
Publicar un comentario